classical probability distribution particle in a box Figure \(\PageIndex{3}\): The probability density distribution \(|\psi_n(x)|^2\) for a quantum particle in a box for: (a) the ground state, \(n = 1\); (b) the first excited state, \(n = 2\); and, (c) the nineteenth excited state, \(n = . We would like to show you a description here but the site won’t allow us.
0 · probability distribution of quantum particle
1 · probability distribution of particle
2 · probability density distribution
3 · particle in a box model
4 · particle in a box diagram
5 · how to find particle in a box
6 · 1 dimensional particle probability
7 · 1 dimensional box particle probability
ShopSabre is home to the most durable and reliable American-made CNC machines. Browse ShopSabre today and find your ideal CNC router or plasma
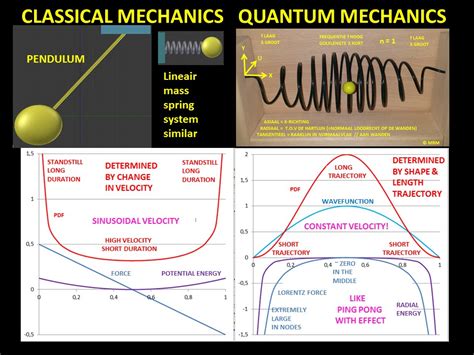
The probability density of finding a classical particle between x and x + Δ x x + Δ x depends on how much time Δ t Δ t the particle spends in this region. Assuming that its speed u is constant, this time is Δ t = Δ x / u, Δ t = Δ x / u, which is also .The simplest form of the particle in a box model considers a one-dimensional system. Here, the particle may only move backwards and forwards along a straight line with impenetrable barriers at either end. The walls of a one-dimensional box may be seen as regions of space with an infinitely large potential energy. Conversely, the interior of the box has a constant, zero pote.This principle states that for large quantum numbers, the laws of quantum physics must give identical results as the laws of classical physics. To illustrate how this principle works for a quantum particle in a box, we plot the probability density . The probability of finding a particle a certain spot in the box is determined by squaring \(\psi\). The probability distribution for a particle in a box at the \(n=1\) and \(n=2\) energy levels looks like this:
Figure \(\PageIndex{3}\): The probability density distribution \(|\psi_n(x)|^2\) for a quantum particle in a box for: (a) the ground state, \(n = 1\); (b) the first excited state, \(n = 2\); and, (c) the nineteenth excited state, \(n = . If you want to compare a classical particle in a box to a quantum model, you'll need to look at two systems with the same total energy, otherwise you're comparing apples .
The probability of finding a particle a certain spot in the box is determined by squaring \(\psi\). The probability distribution for a particle in a box at the \(n=1\) and \(n=2\) energy levels looks like this:This principle states that for large quantum numbers, the laws of quantum physics must give identical results as the laws of classical physics. To illustrate how this principle works for a quantum particle in a box, we plot the probability density .The relative probability distribution, P R (x), for a classical system can be thought of as the amount of time that a particle spends in a small region of space, |dx|, relative to some same .quantum mechanical behavior approaches the classical limit, i.e. the particle would have equal probability of being found anywhere in the box. This is an example of the Bohr .
The probability density of finding a classical particle between x and x + Δ x x + Δ x depends on how much time Δ t Δ t the particle spends in this region. Assuming that its speed u is constant, this time is Δ t = Δ x / u, Δ t = Δ x / u, which is also constant for any location between the walls.In classic physics, the particle can be detected anywhere in the box with equal probability. In quantum mechanics, however, the probability density for finding a particle at a given position is derived from the wave function as P ( x ) = | ψ ( x ) | 2 . {\displaystyle P(x)=|\psi (x)|^{2}.}This principle states that for large quantum numbers, the laws of quantum physics must give identical results as the laws of classical physics. To illustrate how this principle works for a quantum particle in a box, we plot the probability density distribution \[|\psi_n(x)|^2 = \dfrac{2}{L} sin^2 (n\pi x/L) \label{7.50} \] The probability of finding a particle a certain spot in the box is determined by squaring \(\psi\). The probability distribution for a particle in a box at the \(n=1\) and \(n=2\) energy levels looks like this:
Figure \(\PageIndex{3}\): The probability density distribution \(|\psi_n(x)|^2\) for a quantum particle in a box for: (a) the ground state, \(n = 1\); (b) the first excited state, \(n = 2\); and, (c) the nineteenth excited state, \(n = 20\).
probability distribution of quantum particle
probability distribution of particle
If you want to compare a classical particle in a box to a quantum model, you'll need to look at two systems with the same total energy, otherwise you're comparing apples and oranges.The probability of finding a particle a certain spot in the box is determined by squaring \(\psi\). The probability distribution for a particle in a box at the \(n=1\) and \(n=2\) energy levels looks like this:

This principle states that for large quantum numbers, the laws of quantum physics must give identical results as the laws of classical physics. To illustrate how this principle works for a quantum particle in a box, we plot the probability density distribution
The relative probability distribution, P R (x), for a classical system can be thought of as the amount of time that a particle spends in a small region of space, |dx|, relative to some same-sized region of reference.quantum mechanical behavior approaches the classical limit, i.e. the particle would have equal probability of being found anywhere in the box. This is an example of the Bohr Correspondence Principle: In the limit of large quantum number, quantum mechanics approaches classical mechanics. Variations on a Particle in a 1-Dimensional Box: What .The probability density of finding a classical particle between x and x + Δ x x + Δ x depends on how much time Δ t Δ t the particle spends in this region. Assuming that its speed u is constant, this time is Δ t = Δ x / u, Δ t = Δ x / u, which is also constant for any location between the walls.
In classic physics, the particle can be detected anywhere in the box with equal probability. In quantum mechanics, however, the probability density for finding a particle at a given position is derived from the wave function as P ( x ) = | ψ ( x ) | 2 . {\displaystyle P(x)=|\psi (x)|^{2}.}This principle states that for large quantum numbers, the laws of quantum physics must give identical results as the laws of classical physics. To illustrate how this principle works for a quantum particle in a box, we plot the probability density distribution \[|\psi_n(x)|^2 = \dfrac{2}{L} sin^2 (n\pi x/L) \label{7.50} \] The probability of finding a particle a certain spot in the box is determined by squaring \(\psi\). The probability distribution for a particle in a box at the \(n=1\) and \(n=2\) energy levels looks like this:
Figure \(\PageIndex{3}\): The probability density distribution \(|\psi_n(x)|^2\) for a quantum particle in a box for: (a) the ground state, \(n = 1\); (b) the first excited state, \(n = 2\); and, (c) the nineteenth excited state, \(n = 20\). If you want to compare a classical particle in a box to a quantum model, you'll need to look at two systems with the same total energy, otherwise you're comparing apples and oranges.The probability of finding a particle a certain spot in the box is determined by squaring \(\psi\). The probability distribution for a particle in a box at the \(n=1\) and \(n=2\) energy levels looks like this:
This principle states that for large quantum numbers, the laws of quantum physics must give identical results as the laws of classical physics. To illustrate how this principle works for a quantum particle in a box, we plot the probability density distributionThe relative probability distribution, P R (x), for a classical system can be thought of as the amount of time that a particle spends in a small region of space, |dx|, relative to some same-sized region of reference.

probability density distribution

weatherproof electrical junction box cable connector
MTP offers a wide range of precision machining services from CNC turning and milling to Swiss-type CNC screw machines. Thanks to the full line of these machines, we provide 24/7 precision turned product manufacturing for clients in industries such .
classical probability distribution particle in a box|probability distribution of quantum particle