a box witn a top of one metal optimization 390 Optimization Problems 4. An open-top box is made from a 12 by 12 inch piece of cardboard by cutting a square from each corner, and folding up. What should x be to maximize the . Get instant online quote for your metal or plastic CNC machined parts, from rapid prototyping to production. Tolerance down to 0.001 inches. Choose from 100+ materials, 60+ surface finishes. ISO 9001:2015, ISO 13485, ISO14001:2015, IATF 16949:2016 certified. Experience lead times as short as 1 day. Start a New CNC Project!
0 · Study Guide
1 · Solved Optimization Problem A box with an open top is to be
2 · Optimization, volume of a box
3 · Optimization problems with an open
4 · Calculus Optimization Problems SOLUTIONS
5 · Calculus
6 · CHAPTER 34 Optimization Problems
7 · 4.7: Applied Optimization Problems
8 · 4.7 Applied Optimization Problems
9 · 4.5: Optimization Problems
The ability to produce and supply these CNC turned parts on a large scale – or better yet, wholesale, entails several strategic benefits that manufacturers can leverage. Economies of .
2) A metal box (without a top) is to be constructed from a square sheet of metal that is 20 cm on a side by cutting square pieces of the same size from the corners of the sheet and then folding .In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the . In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all .390 Optimization Problems 4. An open-top box is made from a 12 by 12 inch piece of cardboard by cutting a square from each corner, and folding up. What should x be to maximize the .
It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. Consequently, we consider the modified . Write an equation in one variable that represents the value we’re tying to maximize or minimize. Take the derivative, set it equal to to find critical points, and use the first .
Optimization: Maximizing volume. One of the key applications of finding global extrema is in optimizing some quantity, either minimizing or maximizing it. For example, suppose you . A rectangular box with a square base, an open top, and a volume of \(216 in.^3\) is to be constructed. What should the dimensions of the box be to minimize the surface area of .If 00\ \mathrm{cm}^2$ of material is available to make a box with a square base and an open top, find the largest possible volume of the box. The quantity we want to optimize is the .Optimization Problem A box with an open top is to be constructed from a square piece of metal that is 4 m by 4 m, by cutting out a square piece from each corner and bending up the sides. .
2) A metal box (without a top) is to be constructed from a square sheet of metal that is 20 cm on a side by cutting square pieces of the same size from the corners of the sheet and then folding up the sides.In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area.390 Optimization Problems 4. An open-top box is made from a 12 by 12 inch piece of cardboard by cutting a square from each corner, and folding up. What should x be to maximize the volume of the box? 12 12 x x x x x x y x 5. A metal box with two square ends and an open top is to contain a volume of 36 cubic inches. What di-
It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. Consequently, we consider the modified problem of determining which open-topped box with a .
Study Guide

Solved Optimization Problem A box with an open top is to be
Write an equation in one variable that represents the value we’re tying to maximize or minimize. Take the derivative, set it equal to to find critical points, and use the first derivative test to determine where the function is increasing and decreasing.Optimization: Maximizing volume. One of the key applications of finding global extrema is in optimizing some quantity, either minimizing or maximizing it. For example, suppose you wanted to make an open-topped box out of a flat piece of cardboard that is 25" long by 20" wide.

A rectangular box with a square base, an open top, and a volume of \(216 in.^3\) is to be constructed. What should the dimensions of the box be to minimize the surface area of the box? What is the minimum surface area?
If 00\ \mathrm{cm}^2$ of material is available to make a box with a square base and an open top, find the largest possible volume of the box. The quantity we want to optimize is the volume of the box.Optimization Problem A box with an open top is to be constructed from a square piece of metal that is 4 m by 4 m, by cutting out a square piece from each corner and bending up the sides. Find the largest volume that such a box can have.2) A metal box (without a top) is to be constructed from a square sheet of metal that is 20 cm on a side by cutting square pieces of the same size from the corners of the sheet and then folding up the sides.
In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area.390 Optimization Problems 4. An open-top box is made from a 12 by 12 inch piece of cardboard by cutting a square from each corner, and folding up. What should x be to maximize the volume of the box? 12 12 x x x x x x y x 5. A metal box with two square ends and an open top is to contain a volume of 36 cubic inches. What di-
It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. Consequently, we consider the modified problem of determining which open-topped box with a . Write an equation in one variable that represents the value we’re tying to maximize or minimize. Take the derivative, set it equal to to find critical points, and use the first derivative test to determine where the function is increasing and decreasing.Optimization: Maximizing volume. One of the key applications of finding global extrema is in optimizing some quantity, either minimizing or maximizing it. For example, suppose you wanted to make an open-topped box out of a flat piece of cardboard that is 25" long by 20" wide.
A rectangular box with a square base, an open top, and a volume of \(216 in.^3\) is to be constructed. What should the dimensions of the box be to minimize the surface area of the box? What is the minimum surface area?If 00\ \mathrm{cm}^2$ of material is available to make a box with a square base and an open top, find the largest possible volume of the box. The quantity we want to optimize is the volume of the box.
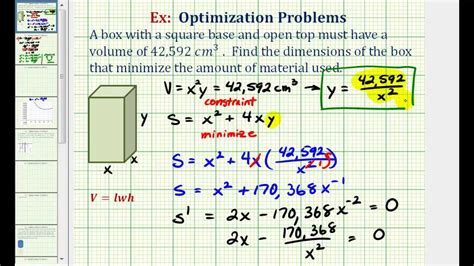
Optimization, volume of a box

caddy box mounting brackets
Grab your bulk pencil pouches and bulk pencil cases at low discounted wholesale prices. Browse all styles, sizes, and colors.
a box witn a top of one metal optimization|4.7 Applied Optimization Problems